QCM Analyse
Si la limite de f en a est inferieur a la limite g en a alors f est inferieur ou egale a g au voisinage de a
Vrai Faux
l'image d'un intervalle ouvert par une fonction continue est un intervalle ouvert
Vrai Faux
Si la limite de la différence de f et g en a est égale à 0 alors f est g sont équivalentes en a
Vrai Faux
Si f est équivalente a 0 en a alors f est nulle au voisinage de a
Vrai Faux
soit f une fonction définie sur l'intervalle fermé a, b dans R et continue et strictement positive alors il existe c positif tel que pour tout x appartenant à cet intervalle la fonction f est supérieure ou égale à c
Vrai Faux
Lim u = 1 en a  lim v = + infini alors lim [ u(x) ]V(x) = 1
lim v = + infini alors lim [ u(x) ]V(x) = 1
 lim v = + infini alors lim [ u(x) ]V(x) = 1
lim v = + infini alors lim [ u(x) ]V(x) = 1
Vrai Faux
Lim u = 0 en a  lim v = + infini en a alors lim [ u(x) ]V(x) = 1
lim v = + infini en a alors lim [ u(x) ]V(x) = 1
 lim v = + infini en a alors lim [ u(x) ]V(x) = 1
lim v = + infini en a alors lim [ u(x) ]V(x) = 1
Vrai Faux
cos x 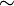 1 + x2/2 en 0
1 + x2/2 en 0
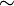 1 + x2/2 en 0
1 + x2/2 en 0
Vrai Faux
lim f(x) = l pour ( x tend vers x0 ) <->  (lim f(x) = l pour ( x tend vers x0- )
(lim f(x) = l pour ( x tend vers x0- )  lim f(x) = l pour ( x tend vers x0+ ))
lim f(x) = l pour ( x tend vers x0+ ))
 (lim f(x) = l pour ( x tend vers x0- )
(lim f(x) = l pour ( x tend vers x0- )  lim f(x) = l pour ( x tend vers x0+ ))
lim f(x) = l pour ( x tend vers x0+ ))
Vrai Faux
 lim ( f - g) en a = 0
lim ( f - g) en a = 0